Ambiguous Grammar & Parse Tree-

We have discussed-

  • Ambiguous Grammar generates at least one string that has more than one parse tree.
  • Parse Tree is the geometrical representation of a derivation.

In this article, we will discuss important points about Ambiguous Grammar and Parse Tree.

Important Points-

Point-01:

  • There always exists a unique parse tree corresponding to each leftmost derivation and rightmost derivation.

If n parse trees exist for any string w, then there will be-

  • n corresponding leftmost derivations.
  • n corresponding rightmost derivations.

Point-02:

For ambiguous grammars,

  • More than one leftmost derivation and more than one rightmost derivation exist for at least one string.
  • Leftmost derivation and rightmost derivation represents different parse trees.

Point-03:

For unambiguous grammars,

  • A unique leftmost derivation and a unique rightmost derivation exist for all the strings.
  • Leftmost derivation and rightmost derivation represents the same parse tree.

Point-04:

  • There may exist derivations for a string which are neither leftmost nor rightmost.

Example

Consider the following grammar-

S → ABC

A → a

B → b

C → c

Consider a string w = abc.

Total 6 derivations exist for string w.

The following 4 derivations are neither leftmost nor rightmost-

Derivation-01:

S → ABC

→ aBC (Using A → a)

→ aBc (Using C → c)

→ abc (Using B → b)

Derivation-02:

S → ABC

→ AbC (Using B → b)

→ abC (Using A → a)

→ abc (Using C → c)

Derivation-03:

S → ABC

→ AbC (Using B → b)

→ Abc (Using C → c)

→ abc (Using A → a)

The other 2 derivations are leftmost derivation and rightmost derivation.

Point-05:

  • Leftmost derivation and rightmost derivation of a string may be exactly same.
  • In fact, there may exist a grammar in which leftmost derivation and rightmost derivation is exactly same for all the strings.

Example

Consider the following grammar-

S → aS / ∈

The language generated by this grammar is-

L = { an , n>=0 } or a*

All the strings generated from this grammar have their leftmost derivation and rightmost derivation exactly same.

Let us consider a string w = aaa.

Leftmost Derivation-

S → aS

→ aaS (Using S → aS)

→ aaaS (Using S → aS)

→ aaa∈

→ aaa

Rightmost Derivation-

S → aS

→ aaS (Using S → aS)

→ aaaS (Using S → aS)

→ aaa∈

→ aaa

Clearly,

Leftmost derivation = Rightmost derivation

Similar is the case for all other strings.

Point-06:

  • For a given parse tree, we may have its leftmost derivation exactly same as rightmost derivation.

Point-07:

  • If for all the strings of a grammar, leftmost derivation is exactly same as rightmost derivation, then that grammar may be ambiguous or unambiguous.

Example

Consider the following grammar-

S → aS / ∈

  • This is an example of an unambiguous grammar.
  • Here, each string have its leftmost derivation and rightmost derivation exactly same.

Now, consider the following grammar-

S → aS / a / ∈

  • This is an example of ambiguous grammar.
  • Here also, each string have its leftmost derivation and rightmost derivation exactly same.

Consider a string w = a.

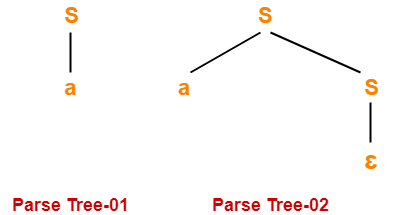
Since two different parse trees exist, so grammar is ambiguous.

Leftmost derivation and rightmost derivation for parse tree-01 are-

S → a

Leftmost derivation and rightmost derivation for parse tree-02 are-

S → aS

S → a∈

S → a

Next Article- Language of Grammar

Get more notes and other study material of Theory of Automata and Computation.

Watch video lectures by visiting our YouTube channel LearnVidFun.

Summary

Ambiguous Grammar | Parse Tree | Important Points

Article Name

Ambiguous Grammar | Parse Tree | Important Points

Description

Important Points about Ambiguous Grammar and Parse Tree- Ambiguous grammar is a grammar whose all strings have exactly one parse tree. Parse tree is a geometrical representation of a derivation.

Author

Akshay Singhal

Publisher Name

Gate Vidyalay

Publisher Logo